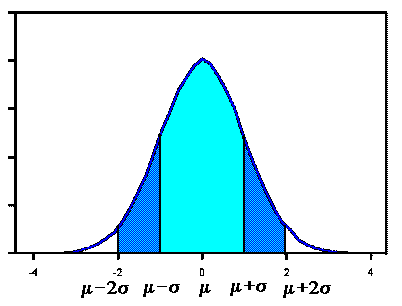
The Standard Normal curve, shown here, has mean 0 and standard deviation 1. If a dataset follows a normal distribution, then about 68% of the observations will fall within  of the mean , which in this case is with the interval (-1,1). About 95% of the observations will fall within 2 standard deviations of the mean, which is the interval (-2,2) for the standard normal, and about 99.7% of the observations will fall within 3 standard deviations of the mean, which corresponds to the interval (-3,3) in this case. Although it may appear as if a normal distribution does not include any values beyond a certain interval, the density is actually positive for all values, 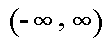. Data from any normal distribution may be transformed into data following the standard normal distribution by subtracting the mean  and dividing by the standard deviation .